Model Zoos for Continual Learning

24 Jun 2022

Consider two tasks: a classification problem between strawberries and raspberries and another classification problem between oranges and bananas. The two tasks are similar and share information relevant to classification. If we can exploit this information, we can achieve lower generalization errors and better sample complexities on both these tasks. This motivates us to explore models that train on multiple tasks.

Caruana’s model (1997) is the most popular choice, when we want to learn from multiple tasks. It relies on learning a shared representation function \(f\) across all the tasks. The output of the function \(f\) is used as input to a task-specific classification layer \(g_i\), to generate predictions for task \(i\). Formally, the classifier for task \(i\) is \begin{equation} h_i := g_i \circ f. \nonumber \end{equation}

In order to tackle our earlier example, we need to learn a single representation \(f\) for oranges, bananas, strawberries and raspberries. For example, we can learn \(f\) using a Resnet backbone. The learnable parameters of \(f\) usually make up most of the parameters in the network since it helps us achieve better sample complexity bounds (Baxter 2000). In addition, we need to learn \(g_1\) and \(g_2\), which are linear layers attached to the Resnet backbone. \(g_1\) is used to identify if the image is a strawberry or a raspberry and \(g_2\) is used to determine if the image is a banana or orange.

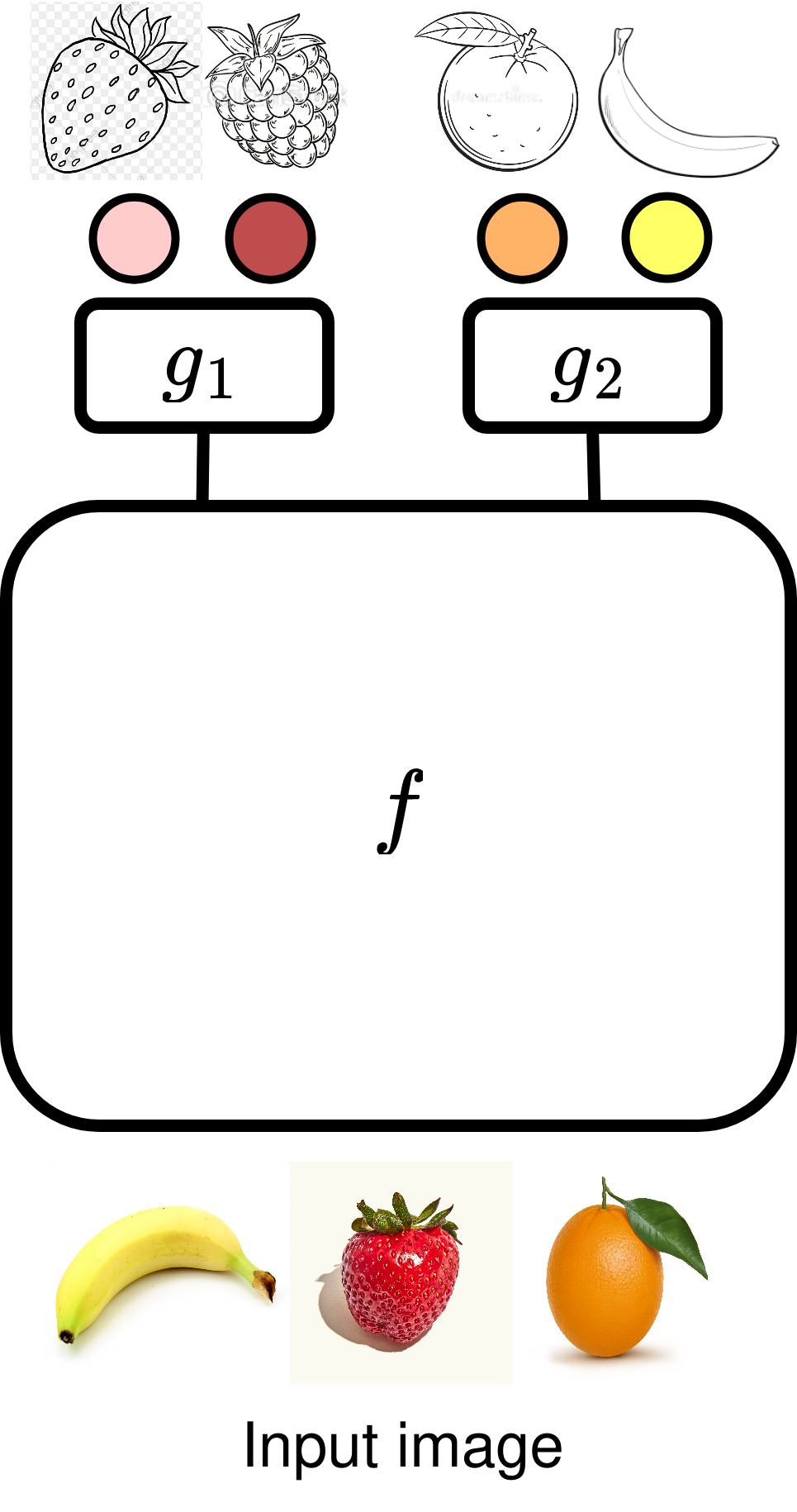
We assume that we know if each image belongs to task 1 or task 2. This helps us choose the right output head for each input. The model need not distinguish between a class from task-1 and another class from task-2. For example, the model need not distinguish between strawberries and oranges since the two classes are from different tasks.

Task-incremental continual learning (Van de Ven and Tolias 2019) studies the problem of learning on a sequence of tasks. The continual learner observes data from a new task after every “episode” of continual learning. We seek low generalization errors on all tasks, observed until the current episode. To achieve this goal, we should leverage information from past tasks, to generalize better on new tasks and simultaneously use information from the new tasks, to improve on past tasks.

What does a typical continual learner look like? Most methods train a single network — one that looks like Caruana’s multi-task model — on a sequence of tasks. At every episode, the network learns to tackle the new task while trying to maintain its ability to address past tasks. The latter is enforced using auxiliary losses or constraints on the gradients.

Task Competition

Caruana’s model assumes that all tasks share a single representation \(f\). This assumption requires all tasks to be similar to each other, which is less likely to be true if we have a large number of tasks. Yet, this model continues to remain the most popular choice architecture, even if we have to tackle many tasks, like in continual learning.

Under Caruana’s multi-task model, we see that tasks can both help and hurt each other. The below matrix is representative of distances between every pair of tasks. It is the decrease (red) or increase (green) in accuracy when we train two tasks together, compared to training on a single task. Clearly, not all pairs of tasks benefit each other – evident from the red cells in the matrix.

We (Ramesh and Chaudhari 2022) formalize this idea using the task-competition theorem. We show that dissimilar tasks fight over the model’s capacity and they benefit from being trained on separate models. This observation inspires us to build Model Zoo, which is capable of expanding its model capacity to accommodate dissimilar tasks.

Model Zoo

Model Zoo (Ramesh and Chaudhari 2022) is a set of models where each model is trained on a subset of tasks. In the continual learning setup, we add 1 model to the zoo after every episode. The model is trained on the new task and a subset of the past tasks (around 2-4). After \(T\) episodes, Model Zoo is consists of an ensemble of \(T\) models, which are each trained on a subset of tasks.

The zoo’s output for a particular task is computed by averaging the outputs of all models trained on that task. For example, the output of the green task is the average of the green output heads of the first two models. The outputs of the orange and yellow tasks can be computed using a single model (orange head of the second model and yellow head of the third model respectively).

Identifying related sets of tasks is the most important component of the zoo; This determines which tasks are trained together. Often, figuring out the relatedness tasks is as expensive as training on those tasks. For continual learning, we seek an inexpensive proxy for the distance between tasks, in order to split the tasks into related subsets.

Inspired by Adaboost, we use the training losses of the tasks to identify which tasks should be trained together. We add a learner to the zoo, which is trained on tasks with high training losses similar to how a Adaboost trains learners on samples with high training errors. Even if the zoo performs poorly on some tasks at episode \(T\), it has the ability to correct itself in future episodes.

Evaluating the Zoo

Continual learning has many formulations which makes it hard to compare different methods. They vary on factors like model storage, sample storage or compute. Methods typically either store no data from previous tasks, or use a limited replay buffer to store a fraction (around 5-10%) of the data from previous tasks. Catastrophic forgetting — a tendency of the model to rapidly forget the solution to past tasks — is commonly observed in these settings and addressing this, is the primary focus of most existing methods.

In our work, we show that a learner that shares no information between the tasks i.e., it does no real continual learning, performs better than existing methods. We call this method Isolated in our work. Isolated has low training times and uses no replay buffer but grows it model capacity linearly with the number of tasks. Existing methods scale well with respect to model size, but fail to achieve good generalization errors.

Model Zoo on the other hand, is able to outperform the Isolated baseline. It improves on previous tasks (backward transfer) and has an improved ability to solve new tasks (forward transfer). The zoo has low training and inference times compared to other methods but grows its model capacity at every episode and uses a replay buffer.

Model Zoo shows that growing the capacity of the model, can help us build effective continual learners. If you are interested in exploring Model Zoos, consider checking out our ICLR 22 paper or this jupyter notebook

References

1. Caruana, Rich. 1997. “Multitask Learning.” Machine Learning 28 (1): 41–75.
2. Baxter, Jonathan. 2000. “A Model of Inductive Bias Learning.” Journal of Artificial Intelligence Research 12: 149–98.
3. Ven, Gido M Van de, and Andreas S Tolias. 2019. “Three Scenarios for Continual Learning.” ArXiv Preprint ArXiv:1904.07734.
4. Ramesh, Rahul, and Pratik Chaudhari. 2022. “Model Zoo: A Growing Brain That Learns Continually.” In International Conference on Learning Representations.